01-(Unirio) Caçador nato, o guepardo é uma espécie de mamífero que reforça a tese de que os animais predadores estão entre os bichos mais velozes da natureza.

Afinal, a velocidade é essencial para os que caçam outras espécies em busca de alimentação. O guepardo é capaz de, saindo do repouso e correndo em linha reta, chegar à velocidade de 72km/h em apenas 2,0 segundos. Determine a aceleração escalar média deste mamífero.
02-(FMTM-MG) Um cientista, estudando a aceleração média de três diferentes carros, obteve os seguintes resultados:
O carro I variou sua velocidade de v para 2v em um intervalo de tempo igual a t;
O carro II variou sua velocidade de v para 3v em um intervalo de tempo igual a 2t;
O carro III variou sua velocidade de v para 5v em um intervalo de tempo igual a 5t.
Sendo, respectivamente, a1, a2 e a3 as acelerações dos carros I, II e III, pode-se afirmar que:
03-(FGV-SP) Um trem desloca-se com velocidade de 72 km/h, quando o maquinista vê um obstáculo à sua frente.

Aciona os freios e pára em 4s. A aceleração média imprimida ao trem pelos freios, foi em módulo, igual a:
04-(PUC-SP) Qual o tempo necessário para que um corpo que acelera a 2 m/s2, partindo do repouso, atinja a velocidade de 108 km/h?
05-(PUC-RS) Uma jogadora de tênis recebe uma bola com velocidade de 20,0m/s e a rebate na mesma direção e em sentido contrário com velocidade de 30,0m/s.

Se a bola permanecer 0,100s em contato com a raquete, o módulo da sua aceleração média será de
06- (CPS-SP) A ampliação da rede de trem metropolitano (metrô) na cidade de São Paulo, visa reduzir o caos do congestionamento urbano, melhorar o transporte coletivo da população e contribuir com a melhoria da qualidade do ar.

Considere uma composição do trem em movimento entre duas estações seguidas, partindo do repouso na Estação Tiradentes e parando na Estação Luz. O esboço gráfico velocidade × tempo que melhor representa o movimento é:
07-(CFT-CE) A seguir, apresentamos um quadro para a comparação da aceleração de alguns veículos. Para todos os casos, o teste foi realizado com os veículos acelerando de 0 a 100 km/h. Observe o tempo necessário para que todos tenham a mesma variação de velocidade:

Tomando como referência o gráfico apresentado, marque a alternativa que indica corretamente o veículo que possui maior aceleração e indique qual a relação, aproximada, entre a sua aceleração e a do veículo de menor aceleração.
a) Parati e 8 vezes maior
b) Parati e 8 vezes menor
c) Corvette e 8 vezes maior
d) Corvette e 8 vezes menor
e) Corvette e 10 vezes maior
08-(UFB) O gráfico abaixo mostra a variação de velocidade de um móvel em função do tempo.

Determine a aceleração escalar média entre 3s e 9s e entre 0 e 12s
09-(PUC-RJ) Um objeto em movimento uniformemente variado tem sua velocidade inicial vo = 0,0 m/s e sua velocidade final vf = 2,0 m/s, em um intervalo de tempo de 4s. A aceleração do objeto, em m/s2, é:
10-(PUC-RS) Medidas referentes ao movimento de uma pequena bola, rolando para baixo pela encosta de um terreno em declive, foram registradas na tabela.
A figura que melhor representa a forma aproximada do terreno referido é:

Movimento acelerado e movimento retardado
11- (UFB) No gráfico anexo está representada a variação da velocidade escalar de um ponto material em função do tempo. Classifique o movimento, em cada trecho em progressivo ou retrógrado, acelerado ou retardado.

12-(UFRJ-RJ) Um móvel em movimento retilíneo tem velocidade escalar variando com o tempo , de acordo com o gráfico.

Podemos afirmar corretamente que entre os instantes:
a) 0 e t12 o movimento é retrógrado acelerado
b) t1 e t2 o movimento é progressivo acelerado
c) t2 e t3 o movimento é retrógrado acelerado
d)) t3 e t4 o móvel está parado
e) t4 e t5 o movimento é progressivo retardado
13-(UNICAMP-SP) O gráfico abaixo representa aproximadamente a velocidade de um atleta

em função do tempo em uma competição olímpica.
a) Em que intervalo de tempo o modulo da aceleração tem o menor valor?
b) Em que intervalo de tempo o modulo da aceleração é máximo?
c) Qual e a distancia percorrida pelo atleta durante os 20s?
d) Qual a velocidade media do atleta durante a competição?
14-(FUVEST-SP) Um trem de metrô parte de uma estação com velocidade escalar constante até atingir, após 10s, a velocidade de 90km/h que é mantida por 30s, para então desacelerar uniformemente durante 10s até parar na estação seguinte.
a) Represente graficamente a velocidade escalar em função do tempo.
b) Calcule a distância entre as duas estações
15-(UFB) Durante um movimento acelerado, qual o sinal da aceleração?
16-(UFMS-MS) Um móvel tem sua velocidade registrada conforme gráfico a seguir. É correto afirmar que

(01) entre 0 e 10s, o movimento é uniforme com velocidade de 43,2 km/h.
(02) entre 10s e 25s, o movimento é uniformemente variado com aceleração de 8,0m/s2.
(04) entre 10s e 25s, o deslocamento do móvel foi de 240m.
(08) entre 0s e 10s, o deslocamento do móvel (em metros) pode ser dado por ΔS = 10t onde t é dado em segundos.
(16) entre 10s e 25s a trajetória do móvel é retilínea.
17- (ENEM) Em uma prova de 100 m rasos, o desempenho típico de um corredor padrão é representado pelo gráfico a seguir:

Em que intervalo de tempo o corredor apresenta ACELERAÇÃO máxima?
a) Entre 0 e 1 segundo.
b) Entre 1 e 5 segundos.
c) Entre 5 e 8 segundos.
d) Entre 8 e 11 segundos.
e) Entre 9 e 15 segundos.
18-(CFT-MG) O gráfico a seguir mostra como varia a velocidade de um móvel, em função do tempo, durante parte do seu movimento.

O movimento representado pelo gráfico pode ser o de uma
a) esfera que desce um plano inclinado e continua rolando por um plano horizontal.
b) fruta caindo de uma árvore.
c) composição de metrô, que se aproxima de uma estação e pára.
d) bala no interior de um cano de arma, logo após o disparo.
19-(CFT-MG) Um ônibus, que trafega em uma via plana, com movimento uniforme, diminuiu sua velocidade até parar, no instante em que o sinal luminoso do semáforo muda para o vermelho. Dentre os gráficos, o que melhor representa esse movimento é

20-(UFMG-MG) O gráfico anexo representa a velocidade escalar de um ponto material em função do tempo. Podemos afirmar que:

a) o gráfico está errado, pois não existe velocidade negativa
b) o deslocamento se processa com velocidade variável, porém sempre no mesmo sentido.
c) o móvel percorreu 3m em um sentido, parou bruscamente, fez percurso igual em sentido contrario e parou bruscamente no ponto de partida.
d) do gráfico apresentado só podemos obter a aceleração escalar do móvel, em função do tempo
21-(PUC-MG)
NA HORA DO ACIDENTE, BRASILEIRO REDUZIA
Eram os instantes finais do segundo bloco do treino classificatório para o GP da Hungria. Felipe Massa tinha o terceiro melhor tempo, mas decidiu abrir uma volta rápida, tentando melhorar, buscando o acerto ideal para o Q3, a parte decisiva da sessão, a luta pela pole position. Percorria a pequena reta entre as curvas 3 e 4 da pista de Hungaroring e começava a reduzir de quase 360 km/h

para 270 km/h quando apagou. Com os pés cravados tanto no freio como no acelerador, não virou o volante para a esquerda, passou por uma faixa de grama, retornou para a pista e percorreu a área de escape até bater de frente na barreira de pneus. Atônito, o autódromo assistiu às cenas sem entender a falta de reação do piloto. O mistério só foi desfeito pelas imagens da câmera on board: uma peça atingiu o flanco esquerdo do capacete, fazendo com que o ferrarista perdesse os reflexos.
Como informado no texto e considerando as aproximações feitas, marque a opção cujo gráfico melhor representa a velocidade do veículo de Felipe Massa em função do tempo.

22-(UERJ-RJ) Um trem de brinquedo, com velocidade inicial de 2 cm/s, é acelerado durante 16 s.

O comportamento da aceleração nesse intervalo de tempo é mostrado no gráfico a seguir.

Calcule, em cm/s, a velocidade do corpo imediatamente após esses 16 s.
23-(UFPR-PR) Para melhor compreender um resultado experimental, quase sempre é conveniente a construção de um gráfico com os dados obtidos. A tabela abaixo contém os dados da velocidade v de um carrinho em movimento retilíneo, em diferentes instantes t, obtidos num experimento de mecânica.

a) Com os dados da tabela acima, faça um gráfico com t (s) representado no eixo x e v (m/s) representado no eixo y. Utilize a
região quadriculada a seguir. (Cada quadrícula tem 0,5 cm de lado.)

b) Com base no gráfico do item (a), descreva o movimento do carrinho.

b) Com base no gráfico do item (a), descreva o movimento do carrinho.
24-(UFRGS-RS) Observe o gráfico a seguir, que mostra a velocidade instantânea V em função do tempo t de um móvel que se desloca em uma trajetória retilínea. Neste gráfico, I, II e III identificam, respectivamente, os intervalos de tempo de 0s a 4s, de 4s a 6s e de 6s a 14s.

Nos intervalos de tempo indicados, as acelerações do móvel valem, em m/s2, respectivamente,
a) 20, 40, e 20.
b) 10, 20 e 5.
c) 10, 0 e -5.
d) -10, 0 e 5.
e) -10, 0 e -5.
25-(UFLA-MG) Dois corpos 1 e 2 realizam um movimento retilíneo. Verifica-se que a variação de velocidade do corpo 1 (Δv1) é o dobro da variação da velocidade do corpo 2 (Δv2), para o mesmo intervalo de tempo Δt. Com relação à aceleração média dos corpos 1 e 2, é CORRETO afirmar que:
26-(UEPA-PA)

A faixa de pedestres é uma conquista do cidadão, a qual vem se consolidando na construção de

novas avenidas nas grandes cidades brasileiras. Um motorista trafegando em uma avenida a 54 km/h observa um pedestre atravessando a faixa e aciona os freios, aplicando uma desaceleração constante no veículo, o qual pára depois de 5 s. Sabendo-se que o motorista conseguiu respeitar a faixa, afirma-se que o coeficiente de atrito entre os pneus e a estrada vale: (Dado: g = 10 m/s2)
a) 0,3
b) 0,5
c) 0,7
d) 0,9
e) 1,1
Resoluções – Movimento acelerado e movimento retardado – aceleração média
01- am=(V – Vo)/(t – to) — am=(72/3,6 – 0)/(2 – 0) — am=10m/s2
02- I- a1=(2v – v)/t — a1=v/t — II – a2=(3v – v)/2t — a2=v/t — III – a3=(5v – v)/5t — a3=4v/5t — R- D
03- am=(0 – 20)/(4 – 0) — am=-5m/s2 — R- C
04-am=(V – Vo)/(t – to) — 2=(108/3,6 – 0)/(t ) — 2=30/(t ) — t=15s
05- Orientando a trajetória, antes de rebater velocidade positiva e depois de rebater, velocidade negativa:

Am=(-30 – 20)/0,1 — am=-50/0,1 — am=-500m/s2 — R- D
06- R- B
07- Menor tempo – maior aceleração – Corvette — am=100/4=25(km/h)/s — maior tempo – menor aceleração – Parati —- am=100/33,35=3(km/h)/s — R- C
08- Entre 3s e 9s — am=(0 – 12)/(9 -3) — am=-12/6 — am=-2m/s2 — entre 0 e 12s — am=(-12 – 6)/(12 – 0) — am=-18/12 — am=- 1,5m/s
09- a=(2 – 0)/(4 – 0) — a=1/2m/s2 — R- B
10- Observe que até 3s a aceleração é constante e vale 3m/s2 (terreno mais inclinado) e que depois ela cai para 2m/s2 (terreno menos inclinado) — R- C
11- Trecho AB — progressivo (V>0) e retardado (o módulo de V está diminuindo, ele vai parar em B “VB=0”)

Trecho BC — retrógrado (V<0) e acelerado (módulo de V está aumentando “em B estava parado”)

Trecho CD — Movimento uniforme com velocidade constante e negativa, portanto retrógrado mas sem aceleração.
Trecho DE — retrógrado (V<0) e retardado (módulo de V está diminuindo “pára em E”)

Trecho EF — progressivo (V>0) e acelerado (módulo de V está aumentando “saiu do repouso em E”)

12- R- C — entre t2 e t3 0 movimento é retrógrado (velocidade negativa) e acelerado (módulo da velocidade está aumentando “estava parado em t2”)
13- a) entre 6s e 16s, a velocidade é constante e a aceleração é nula.
b) entre 0 e 6s (movimento progressivo acelerado)
c) o deslocamento (distância percorrida) em todo gráfico V X t é fornecido pela área entre 0 e 20s — área do triângulo=b.h/2=6.12/2=36m + área do retângulo=b.h=10.12=120m + área do trapézio=(B + b).h/2=(12 + 10).4/2=44m — deslocamento = 36 + 120 + 44 — d=200m
d) Vm=d/t — Vm=200/20 — Vm=10m/s
14- a) V=90/3,6=25m/s
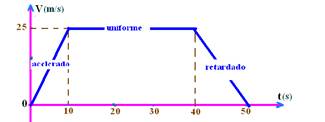
b) A distância é fornecida pela área do trapézio — ΔS=(B + b).h/2=(50 + 30).25/2 — ΔS=1.000m
15- Se o movimento for progressivo o sinal será positivo, mas se o movimento for retrógrado o sinal será negativo.
16- (01) Correta — V é constante e vale 12m/s X 3.6=43,2km/h e o movimento é progressivo (V>0 e a=0)
(02) Falsa — o movimento é uniformemente acelerado mas a aceleração vale a=(20 – 12)/(25 – 10) — a=0,53m/s2
(04) O deslocamento é fornecido pela área do trapézio — ΔS=(20 + 12).15/2 — ΔS=240m — Correta
(08) ΔS=10t=10.10=100m — entre 0 e 10s ΔS é fornecido pela área do retângulo=10.12=120m — Falsa
(16) Falsa — nada se pode afirmar a respeito da trajetória
Soma=(01 + 04) = 05
17- Quanto mais inclinada reta representativa da velocidade maior será a aceleração — R- A
18- R- C — é o único movimento que é retardado com a velocidade diminuindo até que ele pare.
19- R- D
20- Movimento progressivo (indo), ΔS=área do trapézio=(2 + 1).2/2=3m que é a mesma que do movimento retrógrado (voltando) — R- C
21- Observe no enunciado que ele começou a reduzir a velocidade de 360kmh para 270kmh quando apagou — movimento retardado com velocidade diminuendo — R- C
22- Entre 0 e 6s — VI=Vo + aItI=2 + 4.6 — Vi=26 cm/s — entre 6s e 10s — VI=Vo=26cm/s — VII=Vo + aIItII=26 + (-3).4 — VII=14 cm/s — VII=Vo=14 cm/s — VIII=Vo + aIII.tIII=14 + 4.6 — VIII=38 cm/s
23- a) Supondo que nos intervalos de 0 e 4 s e de 12 s a 16 s a velocidade permaneça constante e que, nos intervalos de 4 s a 8 s e de 16 s a 20 s as variações de velocidade sejam constantes, o gráfico pedido está representado abaixo.
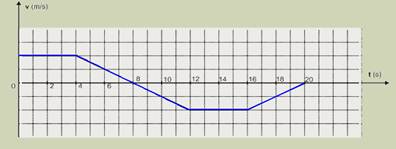
b) Com base no gráfico obtido no item( a) podemos descrever o movimento do carrinho da seguinte maneira:
de t = 0 a t = 4 s o movimento é progressivo e uniforme;
de t = 4 s a t = 8 s o movimento é progressivo e uniformemente retardado;
de t = 8 s a t = 12 s o movimento é retrógrado e uniformemente acelerado;
de t = 12 s a t = 16 s o movimento é retrógrado e uniforme,
de t = 16 s a t = 20 s o movimento é retrógrado e uniformemente retardado.
24- Sendo a trajetória é retilínea, a aceleração restringe-se à componente tangencial  , que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da velocidade (Dv) em relação ao tempo (Dt) — a=ΔV/Δt — para cada intervalo você tem — I. aI=(40 – 0)/(4 – 0) — aI=10m/s2 — II. AII = 0 (não houve variação de velocidade) — III. aIII=(0 – 40)/(14 – 6) —
, que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da velocidade (Dv) em relação ao tempo (Dt) — a=ΔV/Δt — para cada intervalo você tem — I. aI=(40 – 0)/(4 – 0) — aI=10m/s2 — II. AII = 0 (não houve variação de velocidade) — III. aIII=(0 – 40)/(14 – 6) —
aIII= – 5m/s2 — R- C
25- am=ΔV/Δt — como ΔV1=2 ΔV2 — am1=2am2 — R- D
26- Cálculo da aceleração de retardamento do carro — Vo=54km/h/3,6=15m/s — V=0 (pára) — t=5s — V= Vo + a.t — 0
= 15 + a.5 — a= – 3m/s2 (o sinal negativo de a significa que o carro está freando) — em módulo — a=3m/s2 — depois que ele acionou os freios a intensidade da força resultante sobre o carro é a própria força de atrito — FR=Fat — m.a = μ.N — m.a = μ.m.g — 3= μ.10 —
μ = 0,3 — R- A
Nenhum comentário:
Postar um comentário